.ipynb .pdf

repository open issue

Binder JupyterHub

Contents

Forecasting

In this notebook, we shall use the modelling techniques we learned about in the concepts notebook and apply that information to forecast or predict future values of a time series.

Content

• Load Data

• ARIMA manual

• SARIMAX

• Auto ARIMA

• Auto ARIMA with seasonality

• Prophet

• Seasonality Decomposition and trend prediction

# Import dependencies

import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from pmdarima import auto_arima
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
from fbprophet import Prophet
from sklearn.metrics import mean_absolute_error

warnings.filterwarnings("ignore")

Load data

For continuity, we are going to use the same data that we used in the concepts notebook. Scale it down to 30 min samples because training takes a long time otherwise.

metric_df = pd.read_pickle("../data/raw/ts.pkl")
### 30 mins because it gets very difficult to model otherwise
ts = metric_df["value"].astype(float).resample("30min").mean()
sns.set()
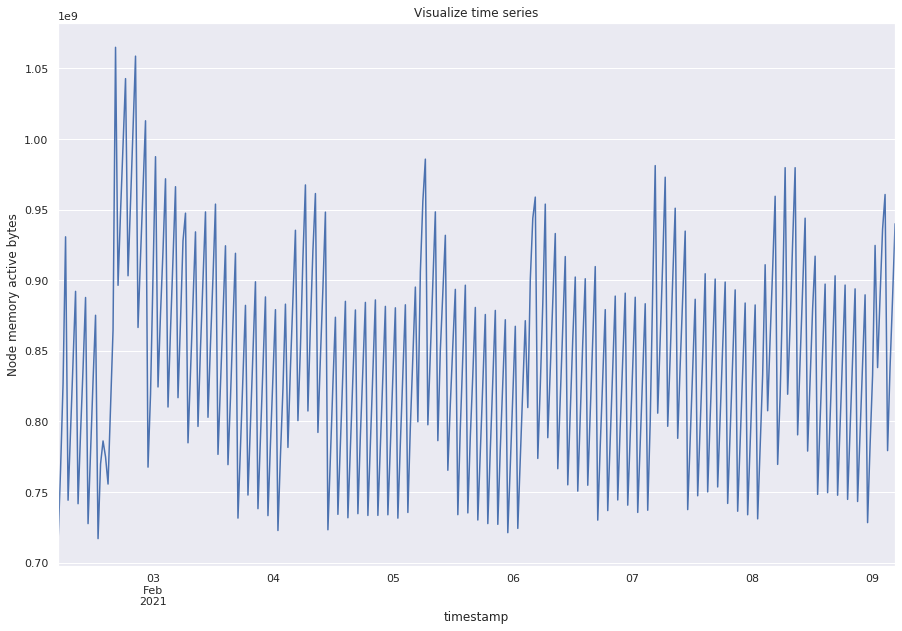
ts.plot(figsize=(15, 10))
plt.title("Visualize time series")
plt.ylabel("Node memory active bytes")
plt.show()

# Divide into train and test set
train = ts[:"2021-02-07"]
test = ts["2021-02-08":]

# Define helper dates
first_date = train.index[0]
sample_date = pd.to_datetime("2021-02-06", utc=True)
start_date = pd.to_datetime("2021-02-08", utc=True)
end_date = pd.to_datetime("2021-02-09", utc=True)

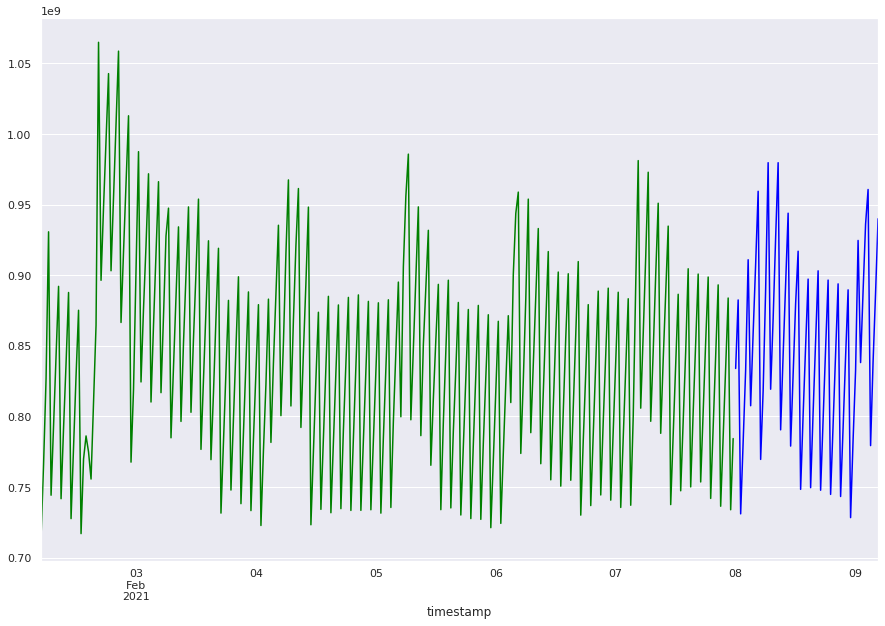
# Plot train and test sets
train.plot(figsize=(15, 10), color="green")
test.plot(figsize=(15, 10), color="blue")

<matplotlib.axes._subplots.AxesSubplot at 0x7fd47ff856d8>

def plot_predicts_aam(pred_train, pred):
    """
    Plots train, test, prediction of training set, and prediction of test set
    for auto arima and fbprophet
    """
    train.plot(figsize=(15, 10), color="green", label="Train actual")

    pd.Series(pred_train, index=train[:start_date].index).plot(
        figsize=(15, 10), color="red", label="Train prediction"
    )

    test.plot(figsize=(15, 10), color="blue", label="Test actual")

    pd.Series(pred, index=test[start_date:].index).plot(
        figsize=(15, 10), color="orange", label="Test prediction"
    )
    plt.legend()
    plt.show()


def plot_predicts_man(pred_train, pred):
    """
    Plots train, test, prediction of training set, and prediction of test set
    for manual ARIMA
    """
    train.plot(figsize=(15, 10), color="green", label="Train actual")

    pred_train.plot(figsize=(15, 10), color="red", label="Train prediction")

    test.plot(figsize=(15, 10), color="blue", label="Test actual")

    pred.plot(figsize=(15, 10), color="orange", label="Test prediction")
    plt.legend()
    plt.show()

Auto Arima

aam_default = auto_arima(train)
pred_aam_default = aam_default.predict(n_periods=len(test))
pred_train_aam_default = aam_default.predict(n_periods=len(train[:start_date]))

aam_default.summary()

SARIMAX Results

Dep. Variable:	y	No. Observations:	278
Model:	SARIMAX(0, 0, 1)	Log Likelihood	-5418.948
Date:	Tue, 06 Apr 2021	AIC	10843.896
Time:	22:27:24	BIC	10854.779
Sample:	0	HQIC	10848.263
	- 278
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
intercept	8.4e+08	6.11e-10	1.38e+18	0.000	8.4e+08	8.4e+08
ma.L1	0.2307	0.067	3.427	0.001	0.099	0.363
sigma2	5.066e+15	1.05e-19	4.82e+34	0.000	5.07e+15	5.07e+15

Ljung-Box (L1) (Q):	0.00	Jarque-Bera (JB):	1.97
Prob(Q):	0.95	Prob(JB):	0.37
Heteroskedasticity (H):	0.68	Skew:	-0.05
Prob(H) (two-sided):	0.06	Kurtosis:	2.60

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 3.47e+51. Standard errors may be unstable.

plot_predicts_aam(pred_train_aam_default, pred_aam_default)

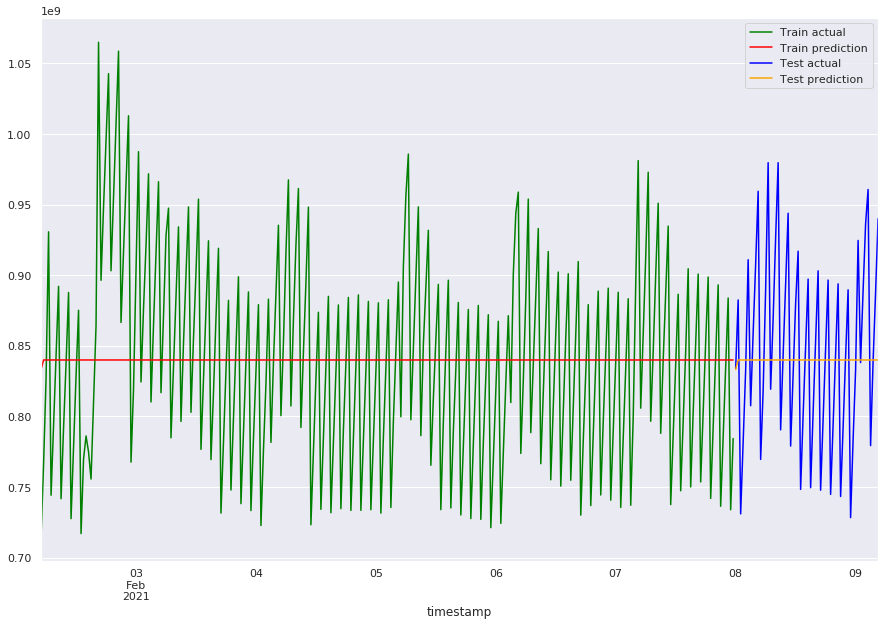
mae_train_aam_default = mean_absolute_error(pred_train_aam_default, train)
mae_aam_default = mean_absolute_error(pred_aam_default, test)
print(f"train error: {mae_train_aam_default}, test error: {mae_aam_default}")

train error: 59704447.00298849, test error: 55499026.40818263

Auto arima with seasonality and trend

aam_tuned = auto_arima(
    train,
    #            exogenous=,
    m=4,  # SARIMAX s
    max_order=None,
    max_p=5,  # Search till p=6
    max_q=5,  # Search till q=6
    max_d=2,  # Search till d=2
    max_P=4,  # Search till P=2
    max_Q=4,  # Search till Q=2
    max_D=2,  # Search till D=2
    maxiter=30,  # Increase if you see no convergence
    njobs=7,  # Number of parallel processes
    trend="ct",  ##ctt for quadratic; accounts for trend in data
    information_criterion="aic",  # out of bag aic, aicc, bic, hqic
    # out_of_sample_size=int(len(ts) * 0.2),  ## Validation set of 20% for oob
)

aam_tuned.summary()

SARIMAX Results

Dep. Variable:	y	No. Observations:	278
Model:	SARIMAX(3, 0, 2)x(0, 0, [1, 2, 3], 4)	Log Likelihood	-5295.031
Date:	Tue, 06 Apr 2021	AIC	10612.062
Time:	22:28:27	BIC	10651.966
Sample:	0	HQIC	10628.071
	- 278
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
intercept	7.802e+08	378.075	2.06e+06	0.000	7.8e+08	7.8e+08
drift	-1.389e+05	5.9e+05	-0.235	0.814	-1.3e+06	1.02e+06
ar.L1	0.5139	0.142	3.628	0.000	0.236	0.792
ar.L2	-0.9205	0.177	-5.200	0.000	-1.267	-0.574
ar.L3	0.5036	0.124	4.051	0.000	0.260	0.747
ma.L1	0.1562	0.222	0.702	0.482	-0.280	0.592
ma.L2	0.9495	0.262	3.628	0.000	0.437	1.462
ma.S.L4	0.6971	0.268	2.605	0.009	0.173	1.221
ma.S.L8	0.6389	0.342	1.871	0.061	-0.030	1.308
ma.S.L12	0.3947	0.252	1.565	0.118	-0.100	0.889
sigma2	4.393e+15	1.78e-06	2.46e+21	0.000	4.39e+15	4.39e+15

Ljung-Box (L1) (Q):	3.20	Jarque-Bera (JB):	1005.96
Prob(Q):	0.07	Prob(JB):	0.00
Heteroskedasticity (H):	0.44	Skew:	1.36
Prob(H) (two-sided):	0.00	Kurtosis:	11.91

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 5.15e+44. Standard errors may be unstable.

pred_aam_tuned = aam_tuned.predict(n_periods=len(test))
pred_train_aam_tuned = aam_tuned.predict(n_periods=len(train[:start_date]))
plot_predicts_aam(pred_train_aam_tuned, pred_aam_tuned)

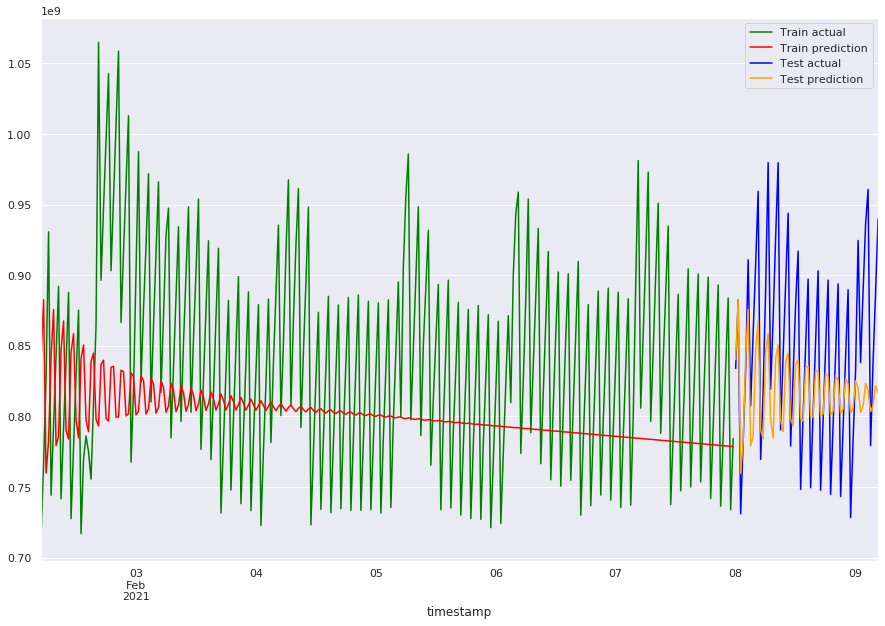
mae_train_aam_tuned = mean_absolute_error(pred_train_aam_tuned, train)
mae_aam_tuned = mean_absolute_error(pred_aam_tuned, test)
print(f"train error: {mae_train_aam_tuned}, test error: {mae_aam_tuned}")

train error: 69104681.4315166, test error: 48501662.87943022

ARIMA manual

first_date = train.index[1]
end_date = test.index[-1]

arima_312 = ARIMA(train, order=(3, 1, 2)).fit()
pred_arima_312 = arima_312.predict(start=start_date, end=end_date)
pred_train_arima_312 = arima_312.predict(start=first_date, end=start_date)
arima_312.summary()

ARIMA Model Results

Dep. Variable:	D.value	No. Observations:	277
Model:	ARIMA(3, 1, 2)	Log Likelihood	-5126.479
Method:	css-mle	S.D. of innovations	25828119.266
Date:	Tue, 06 Apr 2021	AIC	10266.958
Time:	22:28:28	BIC	10292.326
Sample:	02-02-2021	HQIC	10277.137
	- 02-07-2021

	coef	std err	z	P>|z|	[0.025	0.975]
const	2.504e+05	nan	nan	nan	nan	nan
ar.L1.D.value	-1.0033	nan	nan	nan	nan	nan
ar.L2.D.value	-0.9420	0.000	-6697.477	0.000	-0.942	-0.942
ar.L3.D.value	-0.9387	0.000	-7245.019	0.000	-0.939	-0.938
ma.L1.D.value	1.0522	0.047	22.469	0.000	0.960	1.144
ma.L2.D.value	0.0563	0.047	1.201	0.230	-0.036	0.148

Roots

	Real	Imaginary	Modulus	Frequency
AR.1	-1.0000	-0.0000j	1.0000	-0.5000
AR.2	-0.0017	-1.0321j	1.0321	-0.2503
AR.3	-0.0017	+1.0321j	1.0321	0.2503
MA.1	-1.0044	+0.0000j	1.0044	0.5000
MA.2	-17.6740	+0.0000j	17.6740	0.5000

plot_predicts_man(pred_train_arima_312, pred_arima_312)

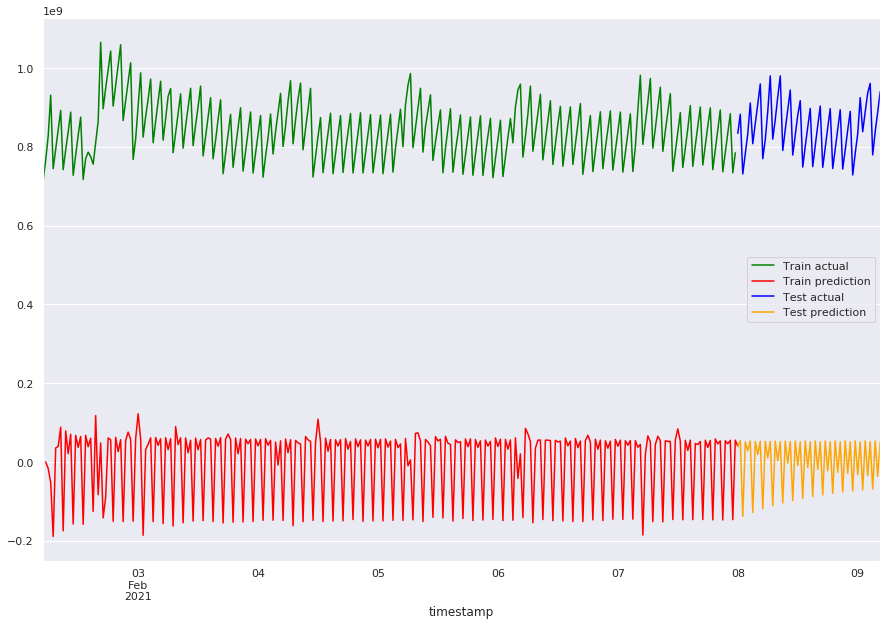
mae_train_arima_312 = mean_absolute_error(pred_train_arima_312, train)
mae_arima_312 = mean_absolute_error(pred_arima_312, test)
print(f"train error: {mae_train_arima_312}, test error: {mae_arima_312}")

train error: 839811151.3563331, test error: 847309633.8738719

arima_313 = ARIMA(train, order=(3, 1, 3)).fit()
pred_arima_313 = arima_313.predict(start=start_date, end=end_date)
pred_train_arima_313 = arima_313.predict(start=first_date, end=start_date)
arima_313.summary()

ARIMA Model Results

Dep. Variable:	D.value	No. Observations:	277
Model:	ARIMA(3, 1, 3)	Log Likelihood	-5056.131
Method:	css-mle	S.D. of innovations	19786859.521
Date:	Tue, 06 Apr 2021	AIC	10128.263
Time:	22:28:34	BIC	10157.255
Sample:	02-02-2021	HQIC	10139.895
	- 02-07-2021

	coef	std err	z	P>|z|	[0.025	0.975]
const	2.504e+05	1.182	2.12e+05	0.000	2.5e+05	2.5e+05
ar.L1.D.value	-1.0004	0.000	-2137.761	0.000	-1.001	-1.000
ar.L2.D.value	-1.0004	0.000	-2138.443	0.000	-1.001	-1.000
ar.L3.D.value	-1.0000	nan	nan	nan	nan	nan
ma.L1.D.value	0.9829	0.008	123.454	0.000	0.967	0.999
ma.L2.D.value	0.9780	nan	nan	nan	nan	nan
ma.L3.D.value	0.9840	nan	nan	nan	nan	nan

Roots

	Real	Imaginary	Modulus	Frequency
AR.1	-1.0000	-0.0000j	1.0000	-0.5000
AR.2	-0.0002	-1.0000j	1.0000	-0.2500
AR.3	-0.0002	+1.0000j	1.0000	0.2500
MA.1	-1.0056	-0.0000j	1.0056	-0.5000
MA.2	0.0058	-1.0053j	1.0053	-0.2491
MA.3	0.0058	+1.0053j	1.0053	0.2491

plot_predicts_man(pred_train_arima_313, pred_arima_313)

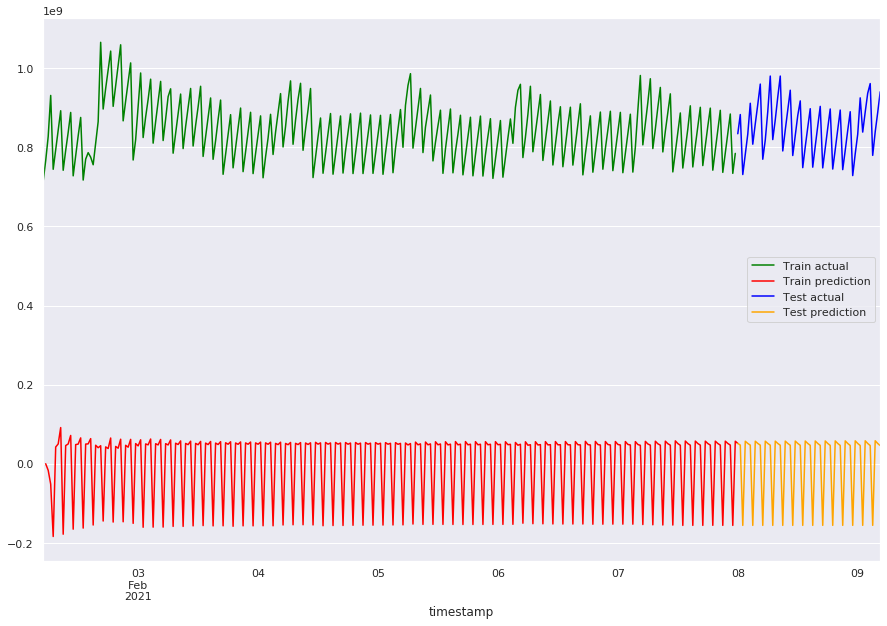
mae_train_arima_313 = mean_absolute_error(pred_train_arima_313, train)
mae_arima_313 = mean_absolute_error(pred_arima_313, test)
print(f"train error: {mae_train_arima_313}, test error: {mae_arima_313}")

train error: 839955467.486684, test error: 846572065.3563603

### SARIMAX

sarima_3133134 = SARIMAX(
    train, order=(3, 1, 3), seasonal_order=(3, 1, 3, 4)
).fit()
pred_sarima_3133134 = sarima_3133134.predict(start=start_date, end=end_date)
pred_train_sarima_3133134 = sarima_3133134.predict(
    start=first_date, end=start_date
)
sarima_3133134.summary()

SARIMAX Results

Dep. Variable:	value	No. Observations:	278
Model:	SARIMAX(3, 1, 3)x(3, 1, 3, 4)	Log Likelihood	-5041.015
Date:	Tue, 06 Apr 2021	AIC	10108.029
Time:	22:28:40	BIC	10154.952
Sample:	02-02-2021	HQIC	10126.865
	- 02-07-2021
Covariance Type:	opg

	coef	std err	z	P>|z|	[0.025	0.975]
ar.L1	0.1141	10.763	0.011	0.992	-20.981	21.209
ar.L2	-0.0459	11.028	-0.004	0.997	-21.661	21.569
ar.L3	-0.0476	8.423	-0.006	0.995	-16.557	16.462
ma.L1	-0.1001	10.746	-0.009	0.993	-21.161	20.961
ma.L2	0.0281	11.041	0.003	0.998	-21.613	21.669
ma.L3	0.0612	8.464	0.007	0.994	-16.527	16.650
ar.S.L4	-0.8363	0.188	-4.452	0.000	-1.205	-0.468
ar.S.L8	0.2501	0.286	0.875	0.381	-0.310	0.810
ar.S.L12	0.5071	0.170	2.978	0.003	0.173	0.841
ma.S.L4	0.5739	0.178	3.226	0.001	0.225	0.923
ma.S.L8	-0.5780	0.174	-3.318	0.001	-0.919	-0.237
ma.S.L12	-0.5949	0.165	-3.605	0.000	-0.918	-0.271
sigma2	8.479e+14	1.93e-12	4.39e+26	0.000	8.48e+14	8.48e+14

Ljung-Box (L1) (Q):	4.34	Jarque-Bera (JB):	3002.25
Prob(Q):	0.04	Prob(JB):	0.00
Heteroskedasticity (H):	0.36	Skew:	0.93
Prob(H) (two-sided):	0.00	Kurtosis:	19.14

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 1.73e+42. Standard errors may be unstable.

plot_predicts_man(pred_train_sarima_3133134, pred_sarima_3133134)

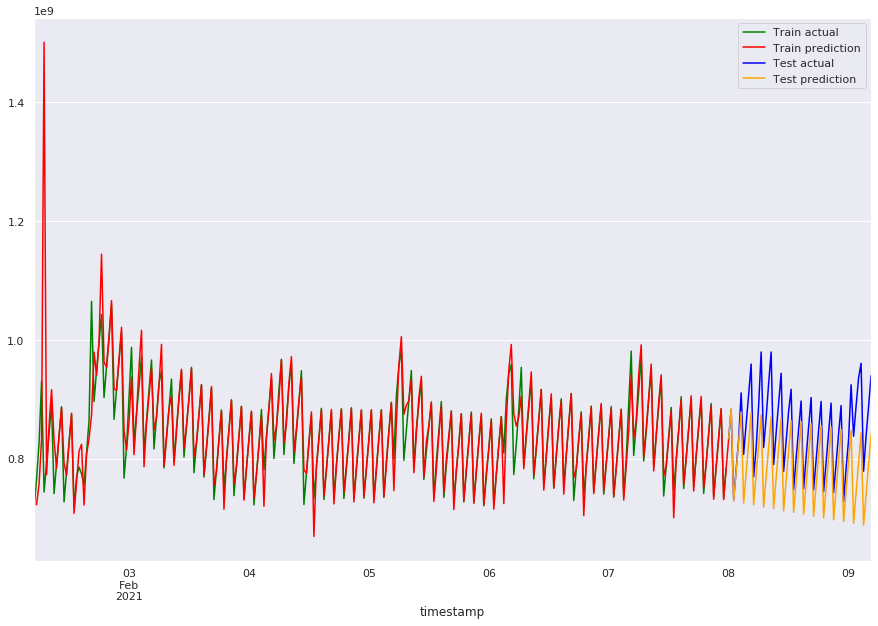
mae_train_sarima_3133134 = mean_absolute_error(
    pred_train_sarima_3133134, train
)
mae_sarima_3133134 = mean_absolute_error(pred_sarima_3133134, test)
print(
    f"train error: {mae_train_sarima_3133134}, test error: {mae_sarima_3133134}"
)

train error: 76039810.8512889, test error: 61440631.127542816

Fb Prophet

• Fb prophet is an open source forecasting tool developed by facebook. It’s working is explained in this paper.

## Convert data to prophet type
train_fb = (
    train.tz_localize(None)
    .reset_index()
    .rename(columns={"timestamp": "ds", "value": "y"})
)
test_fb = (
    test.tz_localize(None)
    .reset_index()
    .rename(columns={"timestamp": "ds", "value": "y"})
)
train_fb

	ds	y
0	2021-02-02 05:00:00	7.149560e+08
1	2021-02-02 05:30:00	7.661634e+08
2	2021-02-02 06:00:00	8.268711e+08
3	2021-02-02 06:30:00	9.307392e+08
4	2021-02-02 07:00:00	7.441884e+08
...	...	...
273	2021-02-07 21:30:00	7.860433e+08
274	2021-02-07 22:00:00	8.343954e+08
275	2021-02-07 22:30:00	8.838431e+08
276	2021-02-07 23:00:00	7.338868e+08
277	2021-02-07 23:30:00	7.843077e+08

278 rows × 2 columns

proph_model = Prophet()
pm = proph_model.fit(train_fb)

INFO:fbprophet:Disabling yearly seasonality. Run prophet with yearly_seasonality=True to override this.
INFO:fbprophet:Disabling weekly seasonality. Run prophet with weekly_seasonality=True to override this.

future = pd.concat([train_fb[["ds"]], test_fb[["ds"]]])
forecast = proph_model.predict(future)
forecast[["ds", "yhat", "yhat_lower", "yhat_upper"]].tail()

	ds	yhat	yhat_lower	yhat_upper
331	2021-02-09 02:30:00	8.159005e+08	7.226906e+08	8.959902e+08
332	2021-02-09 03:00:00	8.249485e+08	7.356618e+08	9.102047e+08
333	2021-02-09 03:30:00	8.335671e+08	7.366603e+08	9.268038e+08
334	2021-02-09 04:00:00	8.408378e+08	7.512273e+08	9.263069e+08
335	2021-02-09 04:30:00	8.461327e+08	7.632898e+08	9.335285e+08

plot_predicts_aam(forecast["yhat"][:278].values, forecast["yhat"][278:].values)

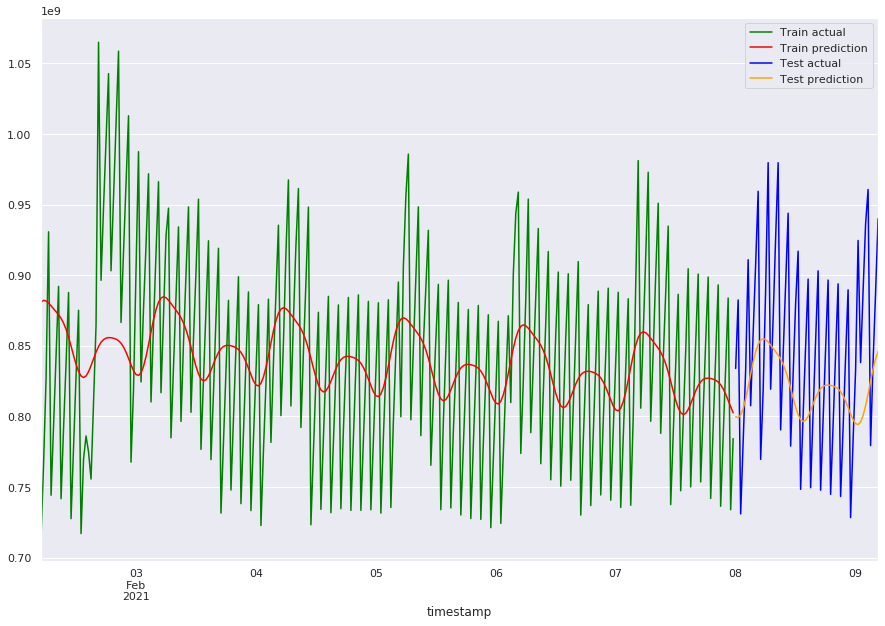
## Prophet finds components as well and forecasts the trend
fig2 = proph_model.plot_components(forecast)

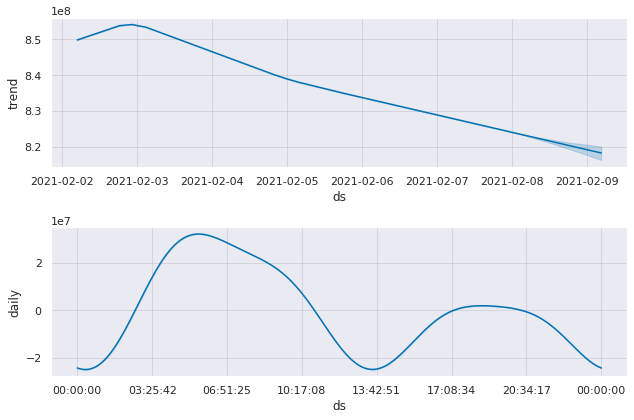
mae_train_prophet = mean_absolute_error(forecast.yhat.iloc[:278], train)
mae_prophet = mean_absolute_error(forecast.yhat.iloc[278:], test)
print(f"train error: {mae_train_prophet}, test error: {mae_prophet}")

train error: 57397365.15948534, test error: 59003779.90772527

Decomposition + trend prediction

• In this method we use the concept of seasonality decomposition. We remove the seasonal component and forecast the adjusted time series. Once we have the forecasted value, we add the seasonality back to the prediction. This method, like SARIMAX, assumes that we have some prior knowledge of the seasons in our time series.

• We use prophet for trend prediction, but any method can be used.

sns.set()
plt.rc("figure", figsize=(15, 10))
sd_add = seasonal_decompose(train, model="additive", freq=2 * 24)
sd_add.plot()
plt.show()

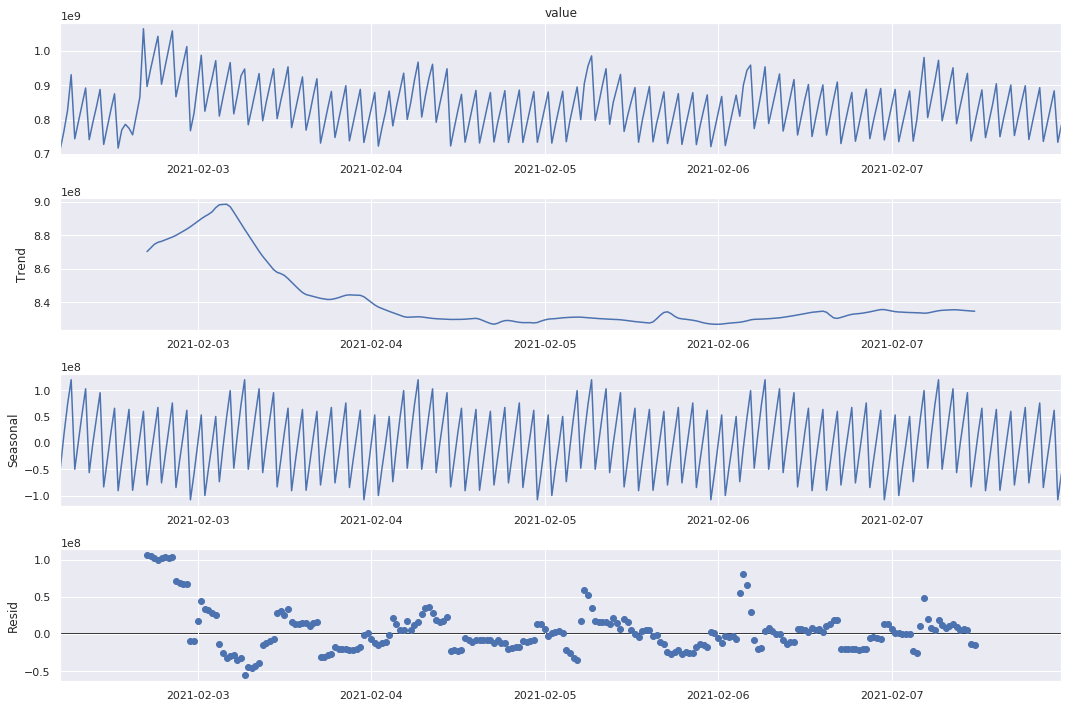
train_adj = train - sd_add.seasonal
train_adj_fb = (
    train_adj.tz_localize(None)
    .reset_index()
    .rename(columns={"timestamp": "ds", 0: "y"})
)
test_fb = (
    test.tz_localize(None)
    .reset_index()
    .rename(columns={"timestamp": "ds", 0: "y"})
)

# Here we take one period from the train decomposed set
# with similar start and end point as the test set
test_set_period_adj = sd_add.seasonal["2021-02-03":"2021-02-04 4:30"]

## Prophet model
proph_model = Prophet()
pm = proph_model.fit(train_adj_fb)
future = pd.concat([train_adj_fb[["ds"]], test_fb[["ds"]]])
forecast = proph_model.predict(future)

INFO:fbprophet:Disabling yearly seasonality. Run prophet with yearly_seasonality=True to override this.
INFO:fbprophet:Disabling weekly seasonality. Run prophet with weekly_seasonality=True to override this.

train_predict_fb_adj = forecast["yhat"][:278].values + sd_add.seasonal.values
predict_fb_adj = forecast["yhat"][278:].values + test_set_period_adj.values
plot_predicts_aam(train_predict_fb_adj, predict_fb_adj)

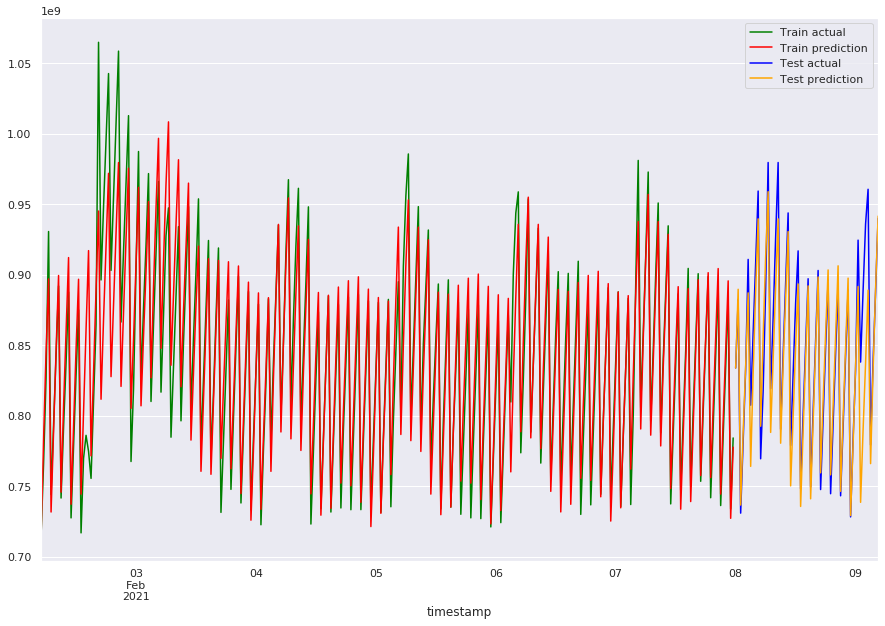
mae_train_fb_adj = mean_absolute_error(train_predict_fb_adj, train)
mae_fb_adj = mean_absolute_error(predict_fb_adj, test)
print(f"train error: {mae_train_fb_adj}, test error: {mae_fb_adj}")

train error: 18666697.80771729, test error: 20050884.18485607

Next, we look at mean absolute errors for all the methods together

pd.DataFrame(
    data=[
        ["aam_default", mae_train_aam_default, mae_aam_default],
        ["aam_tuned", mae_train_aam_tuned, mae_aam_tuned],
        ["arima_312", mae_train_arima_312, mae_arima_312],
        ["ARIMA_313", mae_train_arima_313, mae_arima_313],
        ["sarima_3133134", mae_train_sarima_3133134, mae_sarima_3133134],
        ["prophet", mae_train_prophet, mae_prophet],
        ["decompose+ARIMA", mae_train_fb_adj, mae_fb_adj],
    ],
    columns=["Method", "Train error", "Test error"],
)

	Method	Train error	Test error
0	aam_default	5.970445e+07	5.549903e+07
1	aam_tuned	6.910468e+07	4.850166e+07
2	arima_312	8.398112e+08	8.473096e+08
3	ARIMA_313	8.399555e+08	8.465721e+08
4	sarima_3133134	7.603981e+07	6.144063e+07
5	prophet	5.739737e+07	5.900378e+07
6	decompose+ARIMA	1.866670e+07	2.005088e+07

Conclusion

In this notebook, we saw some frequently explored ways to forecast a time series. In our example, the method with seasonal decomposition and trend prediction using fbprophet perfromed the best. The method of removing the seasonal effects and predicting the trend performs well if your data has obvious seasonality. Prophet is a powerful tool that works well with various types of time series and it’s performance can be increased with using methods like decomposition. For a general dataset, similar experiments need to be conducted to choose a model.

References

• https://machinelearningmastery.com/findings-comparing-classical-and-machine-learning-methods-for-time-series-forecasting/

• https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb

• https://otexts.com/fpp2/

previous

Time series Concepts and modelling